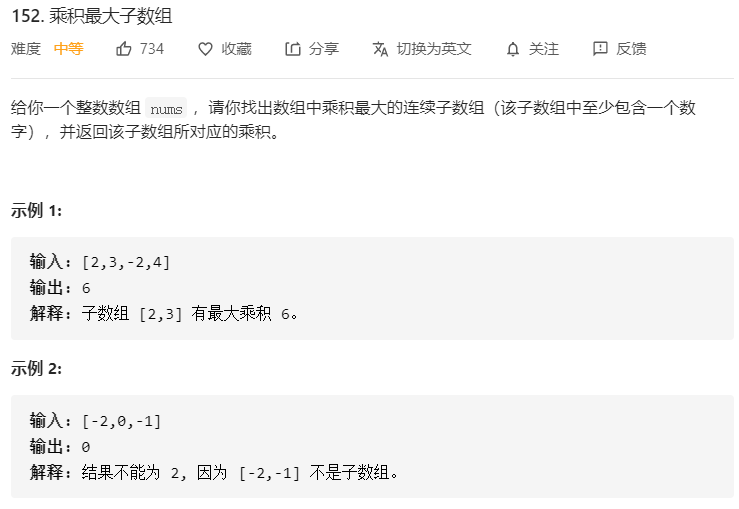
题目分析
这个题目和前两天说的一个最大子序和的题目类似,不过这个题目不是求和而是求积。求和和求积有什么区别呢?为啥这个题目的难度就是中等,而上一个题目的难度是简单呢。求和的题目不会涉及到符号的问题,如果前缀和小于0,则相加时不考虑前缀,这时上一个题目的核心思想。而这个题目的难点在于,可能出现负数乘负数产生正数的情况。
DP
我们使用动态规划进行求解,这时我们不但要记录最大值的状态也要记录最小值的状态,对正数和负数进行分别讨论。dp_max[i]表示右端点选择第i个数可得的最大值,dp_min[i]表示右端点选择第i个数可得的最小值。可以得到状态转移方程
$$dp_max[i] = \begin{case} max(dp_max[i - 1] * nums[i] , nums[i]) & nums[i] > 0 \ nums[i] & max(dp_min[i - 1] * nums[i], nums[i]) \le 0 \end{cases}$$
$$dp_min[i] = \begin{case} min(dp_min[i - 1] * nums[i] , nums[i]) & nums[i] > 0 \ nums[i] & min(dp_max[i - 1] * nums[i], nums[i]) \le 0 \end{cases}$$
当考虑到所有情况后,就可以得到右端点为任何情况下的最大值,然后求dp_max数组的最大值即可。DP的**时间复杂度为$O(n)$,空间复杂度为$O(n)$**。
1 | class Solution(object): |
优化DP
我们发现每次只需要使用到dp_max[i - 1]和dp_min[i - 1],因此可以使用一个变量pre_num保存dp[i - 1],然后实时更新这个变量即可,并且更新同时记录最大值,这样可以节约空间复杂度。这种算法的**时间复杂度为$O(n)$,空间复杂度为$O(1)$**。
1 | class Solution(object): |
刷题总结
这个题目需要和leetcode53题一起做,并且仔细比较两个题目之间的差异,观察状态转移方程的写法。